Для определения единичного вектора нормали (т.е. вектора, перпендикулярного отрезку или плоскости) служит функция nor. Результат функции nor единичный вектор, а не точка. Этот вектор задает направление нормали, а не ее положение в пространстве. Для получения координат конца вектора нормали, исходящего из какой-либо точки, нужно сложить эти точку и вектор.
Определение трехмерного единичного вектора нормали к выбранному кругу, дуге или дуговому сегменту полилинии. Направление вектора нормали совпадает с осью Z объектной системы координат (ОСК) данного объекта.
Определение двумерного единичного вектора нормали к вектору v. Оба вектора считаются двумерными, спроецированными на плоскость XY текущей ПСК. Ориентация вектора нормали такова, что он указывает влево от исходного вектора v.
Определение двумерного единичного вектора нормали к отрезку (p1,p2). Отрезок считается направленным от p1 к p2. Ориентация вектора нормали такова, что он указывает влево от исходного отрезка (p1,p2).
Определение трехмерного единичного вектора нормали к плоскости, проходящей через три точки p1, p2 и p3. Ориентация вектора нормали такова, что при взгляде в направлении вектора три точки расположены против часовой стрелки.
На следующих чертежах проиллюстрированы примеры определения векторов нормалей:
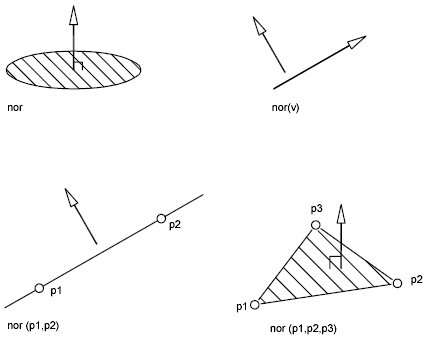
В следующем примере производится установка направления взгляда перпендикулярно выбранному объекту. В программе объект отображается в плане и не искажен параллельной проекцией.
Команда: тзрения
Текущее направление взгляда: VIEWDIR=текущее
Задать точку зрения или [Повернуть] <компас и тройка осей>: 'кальк
>> Выражение: nor
>> Выбрать круг, дугу или полилинию для функции NOR: