Using an attribute extraction template file, you can extract attribute information from a drawing and create a separate text file for use with database software.
You can extract attribute information from a drawing and create a separate text file for use with database software. This feature is useful for creating parts lists with information already entered in the drawing database. Extracting attribute information does not affect the drawing.
To create a parts list
To extract attribute information, you first create an attribute template file using any text processor, then generate the attribute extraction file using AutoCAD, and, finally, open the attribute extraction file in a database application. If you plan to extract the attribute information to a DXF (drawing interchange format) file, it is not necessary to first create an attribute template file.
Create an Attribute Extraction Template File
Before you extract attribute information, you must create an ASCII template file to define the structure of the file that will contain the extracted attribute information. The template file contains information about the tag name, data type, field length, and number of decimal places associated with the information you want to extract.
Each field in the template file extracts information from the block references in the drawing. Each line in the template file specifies one field to be written to the attribute extraction file, including the name of the field, its character width, and its numerical precision. Each record in the attribute extraction file includes all the specified fields in the order given by the template file.
The following template file includes the 15 possible fields. N means numeric, C means character, www means a 3 digit number for the total width of the field, and ddd means a 3 digit number representing how many numeric decimal places are to be displayed to the right of the decimal point.
BL:NAME Cwww000 (Block name)
BL:LEVEL Nwww000 (Block nesting level)
BL:X Nwwwddd(X coordinate of block insertion point)
BL:Y Nwwwddd(Y coordinate of block insertion point)
BL:Z Nwwwddd(Z coordinate of block insertion point)
BL:NUMBER Nwww000 (Block counter; the same for MINSERT)
BL:HANDLE Cwww000 (Block handle; the same for MINSERT)
BL:LAYER Cwww000 (Block insertion layer name)
BL:ORIENT Nwwwddd(Block rotation angle)
BL:XSCALE Nwwwddd(X scale factor)
BL:YSCALE Nwwwddd(Y scale factor)
BL:ZSCALE Nwwwddd(Z scale factor)
BL:XEXTRUDE Nwwwddd(X component of block extrusion direction)
BL:YEXTRUDE Nwwwddd(Y component of block extrusion direction)
BL:ZEXTRUDE Nwwwddd(Z component of block extrusion direction)
numericNwwwddd (Numeric attribute tag)
characterCwww000 (Character attribute tag)
The template file can include any or all of the BL:xxxxxxx field names listed, but must include at least one attribute tag field. The attribute tag fields determine which attributes, hence which blocks, are included in the attribute extraction file. If a block contains some, but not all, of the specified attributes, the values for the absent ones are filled with blanks or zeros, depending on whether the field is a character field or a numeric field.
Comments should not be included in an attribute template file.
The illustration and table show an example of the type of information you're likely to extract, including block name, manufacturer, model number, and cost.
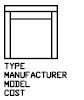
|
Field |
(C)haracter or (N)umeric data |
Maximum field length |
Decimal places |
|---|---|---|---|
|
Block name |
C |
040 |
000 |
|
Manufacturer |
C |
006 |
000 |
|
Model |
C |
015 |
000 |
|
Cost |
N |
006 |
002 |
You can create any number of template files, depending on how you'll use the data. Each line of a template file specifies one field to be written in the attribute extraction file.
Follow these additional guidelines:
The following is a sample template file.
BL:NAME C008000 (Block name, 8 characters)
BL:X N007001 (X coordinate, format nnnnnn.d)
BL:Y N007001 (Y coordinate, format nnnnnn.d)
SUPPLIER C016000 (Manufacturer's name, 16 characters)
MODEL C009000 (Model number, 9 characters)
PRICE N009002 (Unit price, format nnnnnnnn.dd)
Create an Attribute Extraction File
After creating a template file, you can extract the attribute information using one of the following formats:
The CDF format produces a file containing one record for each block reference in a drawing. A comma separates the fields of each record, and single quotation marks enclose the character fields. Some database applications can read this format directly.
The SDF format also produces a file containing one record for each block reference in a drawing. The fields of each record have a fixed width and employ neither field separators nor character-string delimiters. The dBASE III Copy . . . SDF operation also produces SDI-format files. The Append From... SDF operation can read a file in dBASE IV format, which user programs written in FORTRAN can easily process.
DXF produces a subset of the drawing interchange format containing only block reference, attribute, and end-of-sequence objects. This option requires no attribute extraction template. The file extension .dxx distinguishes an extraction file in DXF format from normal DXF files.
Use the Attribute Extraction File
The attribute extraction file lists values and other information for the attribute tags you specified in the template file.
If you specified a CDF format using the sample template, the output might appear as follows:
'DESK', 120.0, 49.5, 'ACME INDUST.', '51-793W', 379.95
'CHAIR', 122.0, 47.0, 'ACME INDUST.', '34-902A', 199.95
'DESK', -77.2, 40.0, 'TOP DRAWER INC.', 'X-52-44',249.95
By default, character fields are enclosed with single quotes (apostrophes). The default field delimeter is a comma. The following two template records can be used to override these defaults:
C:QUOTE c (Character string delimeter)
C:DELIM c (Field delimeter)
The first nonblank character following the C:QUOTE or C:DELIM field name becomes the respective delimiter character. For example, if you want to enclose character strings with double quotes, include the following line in your attribute extraction template file:
C:QUOTE "
The quote delimiter must not be set to a character that can appear in a character field. Similarly, the field delimiter must not be set to a character that can appear in a numeric field.
If you specified an SDF format using the sample template, the file might be similar to the following example.
|
(NAME) |
(X) |
(Y) |
(SUPPLIER) |
(MODEL) |
(PRICE) |
|---|---|---|---|---|---|
|
DESK |
120.0 |
49.5 |
ACME INDUST. |
51-793W |
379.95 |
|
CHAIR |
122.0 |
47.0 |
ACME INDUST. |
34-902A |
199.95 |
|
DESK |
-77.2 |
40.0 |
TOP DRAWER INC. |
X-52-44 |
249.95 |
The order of the fields corresponds to the order of the fields in the template files. You can use these files in other applications, such as spreadsheets, and you can sort and manipulate the data as needed. For example, you can open an attribute extraction file in Microsoft Excel in which you can specify a separate column for each field. See the documentation for your spreadsheet program for information about how to use data from other applications. If you open the file in Notepad or another Windows text processor, you can paste the information back into the drawing as text.
The line BL:LEVEL in a template file reports the nesting level of a block reference. A block that is inserted in a drawing has a nesting level of 1. A block reference that is part of (nested within) another block has a nesting level of 2, and so on.
For a nested block reference, the X,Y, Z coordinate values, scale factors, extrusion direction, and rotation angle reflect the actual location, size, orientation, and rotation of the nested block in the world coordinate system.
In some complex cases, nested block references cannot be correctly represented with only two scale factors and a rotation angle, for example, if a nested block reference is rotated in 3D. When this happens, the scale factors and rotation angle in the extracted file record are set to zero.
If a field is not wide enough for the data that is to be placed in it, the data is truncated and the following message is displayed:
** Field overflow in record <record number>
This could happen, for example, if you have a BL:NAME field with a width of 8 characters and a block in your drawing has a name 10 characters long.